Welcome back to Zigao Wang’s Blog! Today, we’re going to review some essential concepts about trees and binary trees in C++. This post will help you understand the basic concepts, terminology, storage structures, and traversal methods of trees and binary trees.

Basic Concepts of Trees

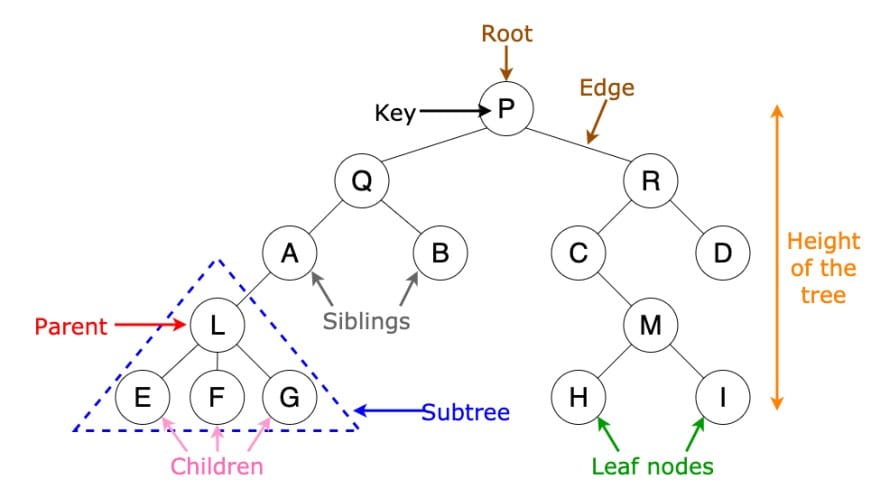
A tree is a non-linear data structure that represents hierarchical relationships. It consists of nodes, where each node can have zero or more child nodes. Nodes without parent nodes are called root nodes, and nodes without child nodes are called leaf nodes.

Basic Terminology of Trees

  • Node: The basic unit of a tree, containing data elements and pointers to its child nodes.
  • Degree of a Node: The number of child nodes a node has.
  • Degree of a Tree: The maximum degree of any node in the tree.
  • Leaf Node: A node with a degree of 0.
  • Non-terminal Node: A node with a degree greater than 0.
  • Child: A lower-level node directly connected to a node.
  • Parent: The immediate higher-level node of a node.
  • Sibling: Nodes that share the same parent.
  • Ancestor: All nodes on the path from the root to a specific node.
  • Descendant: Any node in the subtree rooted at a specific node.
  • Level: The root node is at level 1, and the level of any other node is one more than the level of its parent.
  • Height (or Depth) of a Tree: The maximum level of any node in the tree.
  • Depth and Height of a Node: Depth is the number of edges from the root to the node, and height is the number of edges on the longest path from the node to a leaf.
  • Cousin: Nodes whose parents are at the same level.
  • Ordered Tree: A tree where the children of each node are ordered.
  • Unordered Tree: A tree where the children of each node are not ordered.
  • Full Tree: A tree in which all levels are completely filled.
  • Forest: A collection of disjoint trees.

An diagram showing the different parts of trees

Sequential Storage of Trees: One-Dimensional Array Parent Representation

Using a one-dimensional array to store tree nodes and representing the relationships between nodes through array indices is a common approach. Usually, each node stores the index of its parent node.

Linked Storage of Trees

  • Child Storage Structure: Each node has multiple pointer fields, each pointing to one of its child nodes.
  • Parent-Child Storage Structure: Each node has a pointer to its parent node and an array of pointers to its child nodes.
  • Child-Sibling Storage Structure: Each node has two pointers: one to its first child and another to its right sibling.

Tree Traversal

  • Preorder Traversal: Visit the root node first, then traverse the left subtree, followed by the right subtree.
  • Inorder Traversal: Traverse the left subtree first, then visit the root node, followed by the right subtree.
  • Postorder Traversal: Traverse the left subtree first, then the right subtree, and finally visit the root node.
  • Level-order Traversal: Visit nodes level by level from top to bottom and from left to right.
  • Leaf Node Traversal: Only traverse the leaf nodes.

Concepts and Definitions of Binary Trees

A binary tree is a special form of a tree in which each node has at most two child nodes, usually referred to as the left child and the right child.

Basic Forms of Binary Trees

  • Empty Binary Tree: A binary tree with no nodes.
  • Binary Tree with Only a Root Node.
  • Binary Tree with a Root Node and either Left, Right, or Both Subtrees.

Classification of Binary Trees

  • General Binary Tree: A binary tree with any structure.
  • Full Binary Tree: A binary tree in which every node, except the leaves, has exactly two children.
  • Complete Binary Tree: A binary tree in which all levels are fully filled except possibly for the last level, which is filled from left to right.

Properties of Binary Trees

  1. A binary tree of depth (i) has at most (2^{i-1}) nodes on the (i)th level (i ≥ 1).
  2. A binary tree of depth (k) has at most (2^k - 1) nodes (k ≥ 1).
  3. In any binary tree, if (n_0) is the number of terminal nodes and (n_2) is the number of nodes with two children, then (n_0 = n_2 + 1).

Storage Structures of Binary Trees

Linked Storage

Linked storage is the most common way to store binary trees, as it adapts well to the changing number of nodes in the tree. Each node contains three fields: data, a left pointer, and a right pointer. The left pointer points to the node’s left child, and the right pointer points to the node’s right child.

Here is an example of the linked storage structure in C++:

1
2
3
4
5
6
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

In this example, TreeNode is the structure definition for a binary tree node. It contains an integer data val and two pointers left and right, pointing to the left and right children, respectively.

Sequential Storage

Sequential storage is typically used for complete binary trees or full binary trees because the nodes are arranged in a regular pattern in an array. For a complete binary tree, we can store it in a one-dimensional array in level order. For any element at index (i), its left child is at (2i + 1) and its right child is at (2i + 2) (assuming the array index starts at 0).

For general binary trees, sequential storage is inefficient and wastes a lot of space. Empty positions in the array are usually marked with special values (e.g., nullptr or other marker values).

Note: In practical applications, we prefer linked storage for general binary trees due to its flexibility and space efficiency. Sequential storage is a good choice for complete and full binary trees because of its high efficiency.

I hope this review helps you understand trees and binary trees better. Stay tuned for more posts on data structures and algorithms. Until next time, happy coding!